Andrej Srakar, University of Ljubljana, is the coordinator and Co-Editor of the YoungStatS project. He writes about random matrices in probability and mathematical physics:

We start our YoungStatS short contributions for the IMS Bulletin with a topic from probability theory, namely random matrix theory (RMT). In today’s mathematics, probability has become a foremost area regarding research possibilities. Randomness and stochastic elements can enrich any mathematical theory: algebra, number theory, topology or partial differential equations. Probability theory bridges several areas subject to intense research, such as random geometry deriving from Oded Schramm’s solution of stochastic Loewner’s equation (2000), showing that its solution is a limit of many, if not most, stochastic processes on a plane.

While random matrix theory could be traced back to works by Wishart and James, its real start is usually attributed to influential papers by Eugene Wigner in the 1950s. Wigner suggested that fluctuations in positions of compound nuclei resonances can be described in terms of statistical properties of eigenvalues of very large real symmetric matrices with independent and identically distributed entries. Wigner’s ideas were further substantiated by Freeman J. Dyson who gave important symmetry classification of Hamiltonians, implying the existence of three major symmetry classes of random matrices: orthogonal, unitary and symplectic. He also introduced the circular versions of random matrix ensembles, developed a detailed theory of their spectra, and suggested a model of Brownian motion in random matrices ensembles.

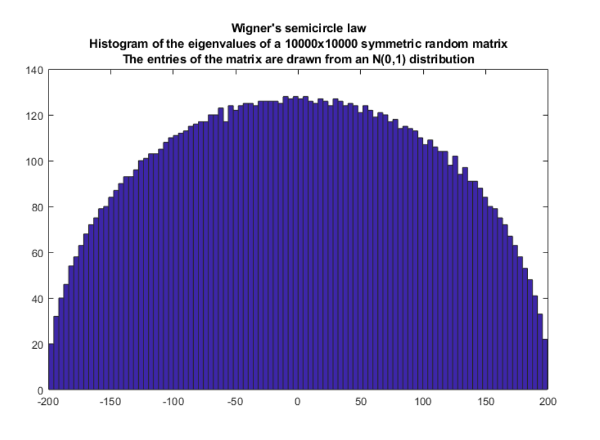
Above: Wigner’s semicircle law for distribution of eigenvalues of a symmetric matrix.
Source: Marco Taboga, https://www.statlect.com/glossary/random-matrix

In two important contributions, Percy Deift listed key open problems in random matrix theory, namely the solution of Korteweg–de Vries equation with almost periodic initial data, universality for random matrices, interacting particle systems in light of the Kardar–Parisi–Zhang universality class, numeric computations with random data, initial boundary value problems for integrable systems and numerical solutions of integrable systems. Important novel probability theory strands such as free probability and traffic probability have emerged, with the first deriving from works of Romanian mathematician Dan-Virgil Voiculescu, being intrinsically connected to many problems in random matrix theory. It introduces a novel concept of independence for random objects, applicable to noncommutative products of random matrices. In recent works, Camille Male introduced an operadic generalization of free probability based on graph operations and motivated by the study of permutation invariant random matrices, and labeled it traffic probability. Independent permutation invariant random matrices provide a canonical model of traffic independence in the large-N limit.

Recent works in random matrix theory address spectra of random graphs, random matrices and related combinatorial problems. There has been great progress in the study of matrices which arise naturally in random graphs, like the adjacency matrix, the Laplacian matrix, or the transition matrix of the random walk on the graph. This relates to the understanding of information contained in eigenvalues and eigenvectors of high-dimensional random matrices. Important are applications of tools stemming from random graphs theory that can be used to study the spectrum of random matrices. Antti Knowles studies eigenvalue problems for Erdős–Rényi and sparse Erdős–Rényi graphs. French mathematician Alice Guionnet studies the theory of large deviations for the spectrum of large random matrices. Also, Gérard Ben Arous studies phase transitions, universality and the spectrum of heavy-tailed random matrices. In an important 2003 article, Romanian American mathematicians Dumitru and Edelman presented a list of open problems for the study of beta ensembles, key objects in random matrix theory. To date, many have remained unaddressed and unresolved.

Study of random matrices features important applications in statistics, data science and econometrics. Frequently, spiked covariance matrices in statistics and econometrics are studied using tools from RMT which forms also the basis of principal component and factor analysis approaches. Development of several machine learning and data science approaches, algorithms and applications is based on random matrix theory. Random matrices can be generalized to random tensors and studied accordingly.

Probability theory is an extremely vibrant and lively field of mathematics. During pandemic time it was the One World Probability seminar, started by Leif Döring and Andreas Kyprianou, which paved the way to a movement of One World online seminars—with 26 such seminars in mathematics to date (including One World YoungStatS). Sometimes, disagreements between probability scholars and statisticians are noted (as noted in Bernard Silverman’s contribution in the August 2022 IMS Bulletin [from his after-dinner speech at last year’s IMS meeting in London]). In the arising artificial intelligence era, which should make the role of mathematics even more pronounced than at present, probability theory is likely to play a highly important, if not a leading role, in developments awaited. At the YoungStatS project we feature two editorial board members active in probability (Lucio Galeati and Andrej Srakar).

We have already published contributions by Balázs Ráth, Jan Swart, Sam Punshon-Smith and Jacopo Borga, among others, and organized several webinars in probability theory. We aim to reflect and steer developments in probability theory, and in random matrices, in the future.