Richard Kenyon received his PhD from Princeton University in 1990 under the direction of William Thurston. After a postdoc at IHES, he held positions at CNRS in Grenoble, Lyon, and Orsay and then became professor at UBC, Brown University and then Yale where he is currently Erastus L. Deforest Professor of Mathematics. He was awarded the CNRS bronze medal, the Rollo Davidson prize, the Loève prize, is a member of the American Academy of Arts and Sciences, and is a Simons Investigator. This Medallion lecture will be delivered at the 43rd Conference on Stochastic Processes and their Applications (SPA) in Lisbon, Portugal, July 24–28, 2023: https://www.spa2023.org/

Dimers, webs and SL₃

The dimer model, or domino tiling model, is the study of the set of dimer covers (also called perfect matchings), of a planar graph or graph on a surface. It is a very successful combinatorial and probabilistic model with connections to the Grassmannian, conformal field theory and integrable systems. The dimer model on the square grid was the first stat mech model rigorously shown, in 2000, to have a conformally invariant scaling limit.

A double dimer cover is obtained by superimposing two dimer covers, to get a collection of loops and doubled edges. In 2011, with David Wilson we studied boundary connection probabilities for the double dimer model in planar graphs, giving the probabilities of the different ways in which boundary points could be connected by chains of double-dimers. These probabilities can be computed from the so-called boundary measurement matrix, or reduced Kasteleyn matrix. As application of the scaling limit of these probabilities, one can compute connection probabilities for multiple SLE₄ curves in the disk. These calculations implicitly use an SL₂-structure on the underlying surface. It is natural to ask about n-fold dimer analogs, and the corresponding SL_n-structures. A union of n dimer covers of a single graph makes a more complicated structure called a graph ical n-web, or n-multiweb. With Daniel Douglas and Haolin Shi we extended the Kasteleyn theory to SL_n-structures, giving enumerative results on n-fold dimers.

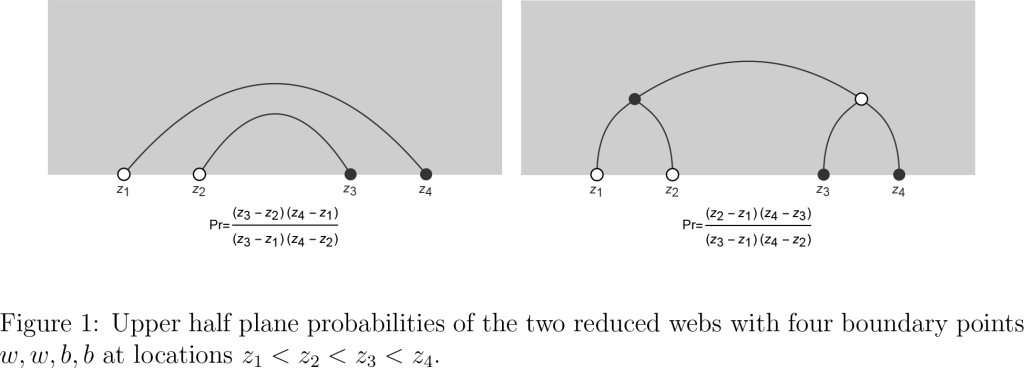
The case n=3 turns out to be simpler than the case of general n because of the notion (originally due to Kuperberg) of “reduced” webs. New results (joint with Haolin Shi) show how to compute the probabilities, and their scaling limits, of reduced 3-webs in the triple dimer model. An example is shown in the figure below.