Congratulations to Mirza Uzair Baig at the University of Hawai’i at Mānoa, who wrote an excellent solution to the problem.

Note that the statistic T_n may be represented as

\[ T_n = I_{Y_{(1)} < X_{(1)}, Y_{(n)} < X_{(n)}}\, \bigg [\sum_{i = 1}^n I_{Y_i < X_{(1)}} + \sum_{i = 1}^n I_{X_i > Y_{(n)}}\bigg ]\]
\[+ \,I_{X_{(1)} < Y_{(1)}, X_{(n)} < Y_{(n)}}\, \bigg [\sum_{ i = 1}^n I_{X_i < Y_{(1)}} + \sum_{i = 1}^n I_{Y_i > X_{(n)}}\bigg ].\]

Denote the empirical CDF of $X_1, \cdots , X_n$ by $F_n$ and that of $Y_1, \cdots , Y_n$ by $G_n$. Then, this above representation yields

\[ T_n = n\,I_{Y_{(1)} < X_{(1)}, Y_{(n)} < X_{(n)}}\, \bigg [G_n(X_{(1)}) +1-F_n(Y_{(n)})\bigg ]\] \[ +\,n\,I_{X_{(1)} < Y_{(1)}, X_{(n)} < Y_{(n)}}\, \bigg [F_n(Y_{(1)}) +1-G_n(X_{(n)})\bigg ].\] Use the fact that for given $u, v, nF_n(u)$ and $nG_n(v)$ are binomial random variables with success probabilities $F(u)$ and $G(v)$. Now use the iterated expectation formula by conditioning on the minima and the maxima to get the mean, and similarly, but with a longer calculation, the variance. It is useful to think of $T_n$ as approximately a sum of two geometrics. Suppose $W$ is a negative binomial with parameters $r = 2, p = \frac{1}{2}$. Then for $n$ not too small, $T_n$ would have a point mass at zero mixed with the negative binomial. That is, write down a Bernoulii variable $Z$ with parameter $\frac{1}{2}$; then $T_n$ (in law) is approximately $Z\,(W+2)$. This gives a quick explanation for why the mean and the variance under the null of $T_n$ should be about $2$ and $6$. You can see a plot below of the null distribution of $T_n$ below when $n = 300$; it is distribution-free in its usual sense.

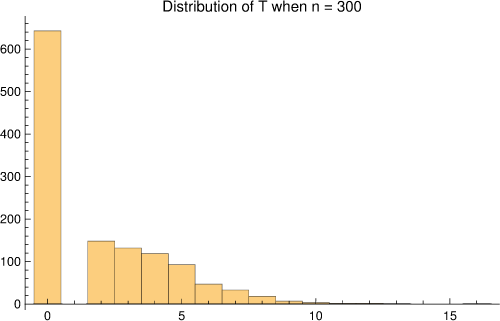
Under specified alternatives, the negative binomial would be replaced by a sum of two geometrics, approximately independent, but not i.i.d.

—

The next puzzle, number 21, is here. Can you solve it? Send us your answer by September 7.