As you may recall from the previous issue, Xiao-Li Meng promised to reveal how a statistician like him found a path to partnering with leaders in the wine industry. All will be revealed in this and the following two installments of the XL-Files. Here, we are reprinting—with permission and with some variations—Xiao-Li’s first publication in a wine magazine, FONDATA, titled Seeking simplicity in statistics, complexity in wine, and everything else in fortune cookies. As Xiao-Li says, “Great wine is meant to be shared and savored with reflection. This bottle pours in three glasses. Cheers!”
Wine and Statistics?
“Since statistics is applicable to almost anything, why not teach a class applying statistics to wine?” Such was the question posed by Wee Lee, a stat—you guessed it—student over an unmemorable bottle during a post-seminar reception back in 2005. Post-seminar receptions are common in academia. They are intended to encourage informal discussions inspired by the seminar, although sometimes I wish that the wines were served before the seminar. The speaker could then be more inspiring, or at least one could blame the wine for the snoring heard throughout the talk. Wee Lee was clearly inspired by the intermingling of wine and statistics, even though the seminar was as unmemorable as the bottle.
How could I have said no to such an inspiration, especially when I had just acquired half of a wine club’s inventory through a liquidation sale? As a pure academic, I was not then and am not now commonly given the resources or opportunity to acquire any fraction of any wine club’s inventory, if the club owner took some statistics courses and understood the risk of running a business. But a club’s loss is an academic’s gain, the latter of which was increased by the wine club salesman’s appreciation of my curiosity about everything wine. “I’d rather give all the remaining bottles to someone who appreciates wine for two dollars a bottle, than have them confiscated tomorrow,” he remarked. It was a subzero evening, but the salesman’s resentment of some prospective almighty confiscator added a couple of real zeros to my wine budget. It’s unclear if the “two dollars a bottle” qualification was his offer or valuation of my appreciation level. But either way, I joined—or rather, closed—the club, in a serendipitous turn of events for a wine-connoisseur-wannabe that ultimately became a singularity for a stat-pedagogue would-be.
(No, you are not tipsy. Yes, this is a story of mixology of enology and pedagogy. Pour yourself another full glass and sip slowly to give me time to regale you.)
Naturally, I could not possibly have kept all this fortune to myself. Lucky fortune cookies are meant to be shared, just as are memorable bottles—memories last far longer by having multiple copies. As a statistics professor, how could I have found a more appropriate use of my newfound fortune than to enhance the lovability of my beloved subject? In case you are not sufficiently aged to appreciate this rhetorical question, there was a time when the answer “I teach statistics” was a very effective turn-off line whenever I was too tired to converse with a taxi driver or a fellow passenger. That effectiveness naturally provoked me. How could statistics be taught in such a way that someday that line would be an invitation?
There was also a time when the concept of a wine cellar was, well, just a concept. I had to move a car out of my garage during that winter when the salesman drove a loaded car into it with almost flat tires. I then moved the bottles into a basement closet as temperatures rose. Attempting to control the temperature in the closet, I installed something that I would rather not disclose unless I want to lose any remaining credibility.
Retrospectively, my laughable attempt could not be a more potent reminder of the critical importance of broad education. As a major in pure mathematics, I had ventured into only one “impure” course during my college years: “Mathematical Equations for Physics.” My descent into impurity prompted inquiry on the part of a few pure-math professors: “Why did you take that?” Of course, they could not have possibly anticipated or understood that even these impure equations did not prepare me for a simple thermodynamic application in real life. I hope that the generous salesman who delivered the bottles will never read this partial confession of torturing his two buck chucks, and hear their whining, “Drink me now, please, to put me out of this misery…”
I, of course, would not do the same to my students. Wee Lee’s inspiration ultimately led to a General Education course at Harvard: Real-Life Statistics: Your Chance for Happiness (or Misery). (As a considerate professor, I always give my students’ choices to accommodate their preferences.) Traditional intro-level statistical courses arrange the content by mathematical and statistical difficulty and bring in stylized examples to illustrate how to apply formulas and carry out computation. The “Happy Course” breaks with this longstanding, common practice, literally and figuratively. The course offered six modules—Romance, Finance, Medical, Election, Legal, and Wine and Chocolate—made possible by my “Happy Team,” a group of graduate students who worked (e.g., dined and wined) with me to develop and deploy the Happy Course. Many pedagogical ideas were fermented over equally many bottles and reified through experiments conducted over several years. Statistical ideas and methods are brought in only when they are needed to address real problems. (In case you want to be amused by “unreal” problems in some stat textbooks, imagine a shoe store owner interested in knowing only the average shoe size the store carries.) This led to the ordering and presentation of technical materials that were unacceptable in the traditional framework.
For example, to understand how “romantic regression”—a Freudian slippery term as romance rarely can escape from its slippery regressing slope—is employed by online dating sites to find your soulmate, the Happy Course introduced logistic regression, used to predict match versus no match, before linear regression. Linear regression is almost always taught before logistic regression in statistics because mathematically the straight lines are easier to teach and understand than the non-linear logistic curves. The concept of linear regressions is used extensively in finance, among many subjects. For example, the notion of high alpha and low beta stocks is built on the intercept (alpha, a measure of return) and slope (beta, a measure of risk) of a linear regression. Seekers of romance may indeed need to learn about linear regression first because money can help to prolong a romance even if it cannot buy one. But the argument that finance must come before romance, because of the mathematical ordering from line to curve, would hardly spark any interest, let alone love, from those students who fear anything mathematical in the first place.
And yes, there are plenty of students—and indeed faculty and deans—at every university and college who consider math to be synonymous with “aftermath.” Teaching stat as a math subject has undoubtedly helped to turn an otherwise intoxicating subject into a conversation terminator, at least before the term Big Data became a headline.
Wine can help, as usual. Some of the most difficult conversations that I had to engage in with my colleagues, in my role as a department chair or graduate school dean, were made a bit more palatable by a bottle or two. Bringing wine into classrooms to ease some fear of math, then, is not a far-fetched idea, especially with the help of the Happy Team. Of course, as a reminder of the statistical wisdom to always expect a bit of everything, I underestimated both the joy generated and the job required by this singular adventure in statistical education.
Wine Tasting and Testing
Wine tasting provides a pedagogically engaging activity to demonstrate the essences and importance of experimental design, a gold standard for making causal conclusions, from clinical trials for treatment efficacy to safety assessments of autonomous vehicles. The myriad of factors influencing wine quality and consumer preference require heedful designs to differentiate and distill them scientifically. Sharing my fortune via wine tasting therefore was almost my first thought upon hearing Wee Lee’s proposal.
As it happened, the half club I inherited consisted of mostly German Riesling, with every possible level of sweetness, from Kabinett to Trockenbeerenauslese. Common wisdom has it that Riesling tends to be the favorite for newbies to wine, or at least the most easily accepted because of its pleasing sweetness. Having introduced several colleagues and friends to the world of wine, my anecdotal observations supported that wisdom. However, anecdotes are not scientific data. If sweetness is an attractor, then it might induce different level of preferences for the different types of the Riesling. To test if this hypothesis is reasonable, one may conduct a wine tasting. But to make it scientific, one must adhere to several principles of experimental design. The obvious one is that it needs to be a blind tasting, just as clinical trials need to be double-blind (i.e., neither patients nor doctors are informed about which patients receive which treatments) whenever feasible. This principle of blindness is to ensure that our scientific vision is not blurred by our judgment’s vulnerability to, for example, label information or price tag. Wine tasting perhaps has the most dramatic and consequential testimony to offer to support this principle. It would take unimaginably many bottles to imagine that the 1976 Judgment of Paris would have reached the same verdict, one which revolutionized the wine world, if it were un-blind.

The tasters tested three kinds of Riesling, in different orderings
The principle of randomization, however, might be less obvious because many people equate randomness with haphazardness. In experimental designs—and in all statistical theory and methods—randomization is the opposite of a haphazard process because randomization means the process is under human control and we know precisely what can happen and how frequently it happens. A typical randomization requires that everyone, or every possibility, be given an equal chance. For comparing different wines, the order of tasting can influence our judgment. (“Never serve your trophy as the third bottle” was a piece of advice given to me last century over a most memorable lunch, but perhaps not to the host, who ultimately thought his office was his bedroom). A well-designed tasting experiment therefore will assign approximately the same number of tasters to every possible order. In the Happy Course’s Riesling tasting, we served three kinds of wine (with all bottles wrapped), resulting in six possible orderings. We had 23 tasters, and hence each order was given to four tasters except for one — see the accompanying photo and slide [below].
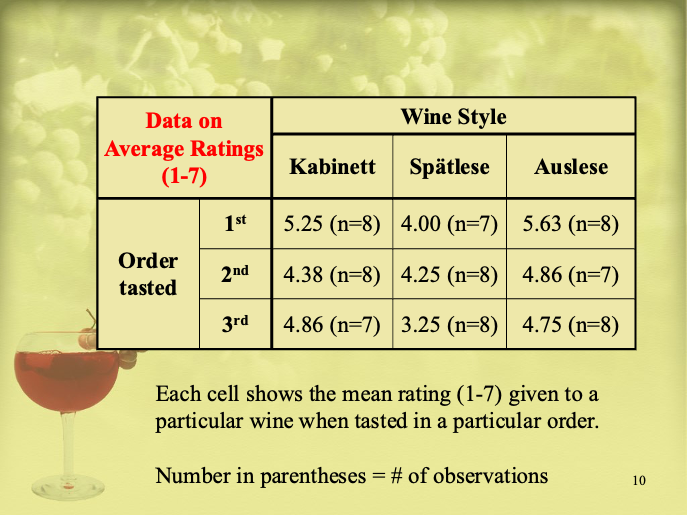
What can be deduced from this data?
(It is probably a good test to see if you need another glass: can you immediately tell which order was the exception?)
The slide was from the actual lecture, where the table documented the average rating for any wine-order combination. I’m not showing the rest of (many) slides, which would easily be your reading terminator. But if your glass still is half full, I’d invite you to pair the half glass with a half number game: What can I conclude from these numbers? Let’s see. Looks like there is an ordering effect, since the two highest average ratings all occurred in the first row. But then the second lowest average rating also occurred in the first row. Wait. The whole Spätlese column received the three lowest ratings, and the first and second average ratings are much closer than that of Kabinett or Auslese. Perhaps then it is OK to declare an ordering effect since these averages were all based on a handful of tasters, and hence we should permit some degree of give-or-take? But what degree is acceptable, and how would that be determined?
Well, that’s why I invited you to play only a half number game, because these averages don’t tell the whole story. How much give-or-take should be allowed will depend on how individual ratings differ from the averages (or equivalently from each other). The more they differ, the more give-or-take results; larger individual differences suggest rather different preference ratings if we had different 23 tasters, or even the same 23 tasters with the same tasting but for a different ordering assignment. Hence, we need to give ourselves more slack to reduce our overconfidence from a single experiment, however scientific it might be.
In case my stat preaching is getting you dizzy (instead of tipsy), let me stop here to say that the actual statistical analysis is simpler and less confusing than ad hoc number games because they follow well specified probability rules and can be carried out by computer (but of course only in the hands of sober trained professionals). As a matter of fact, the whole idea of statistical analysis and more broadly data science is to help humans navigate mind-boggling “number games” created by complex problems—judging wine quality and understanding consumer preferences is one of them. We can then see the big picture and act on essences, instead of getting lost in a maze or jungle. Through pedagogical activities such as wine tasting, the students in the Happy Course got a direct taste of how real-life statistics help to reveal simplicity within and from complexity, a process—perhaps ironically—not unlike seeking complexity out of seemingly simple fermented grape juice, because both processes require training, practicing, understanding, judging, and a bit of luck.
—
The next serving of XL-Files features an experiment with a double dose of happiness: wine… AND chocolate!