Ruobin Gong, Rutgers University, writes:
Suppose that you and a group of friends play the following game. Everybody guesses an integer between 1 and 100. You win by getting closest to half of the median sample of guesses, and the winner takes home the dollar amount s/he had guessed. What number would you guess?
In the winter of 2011, the then department Chair Xiao-Li Meng entertained the crowd gathered at the Harvard statistics holiday party with the above game. It turned out that of all the guesses, the median was 13, and two guesses—five and eight—came closest to half of that. Hillel Bavli, a fellow student and now a professor of Law at SMU, and I were tied as winners, both pleasantly surprised to take home a cheque cut to us by the Chair himself.
I never cashed that $8 cheque; it reminds me of the inspirational and fun time at Harvard. The game we played was in fact a variant of a classic puzzle in game theory called “Guess 2/3 of the average” [3]. To many of us students in the room, this was a first—and a vivid—demonstration. As the name suggests, in this classic setting the participants would aim at 2/3 of the average by guessing a real number in [0, 100]. The winner would take home a prize of a pre-determined amount. (At parties, one can spice things up by letting the winning guess determine the prize amount. Median is also preferred to the mean since it is easier to tabulate manually.)
The catch is this. If all participants were not only perfectly rational, but also know so of all others, the optimal winning strategy for the classic setting is for everyone to guess zero. In reality however, neither assumption is true: we not only depart from rationality, but know others will, too. A realistic winning strategy must be calibrated to the pool of opponents with whom one is sharing the fun, and that can vary substantially from sample to sample. The Danish newspaper Politiken [2] and The New York Times [1] both tried this game on large pools of readers, with 19,196 and 56,000 respondents, and winning guesses of 21.6 and 19, respectively.
How does one come up with a sample-calibrated strategy? There is one mental path many typically follow, with or without knowing. The player begins by estimating the number of “steps” (denoted by κ) by which the opponents are thinking ahead. The most naïve opponent thinks κ = 0 step ahead, and guesses completely randomly. Thus, a roomful of “step 0” opponents would likely produce a median guess around 50. To win against them, one needs to think κ = 1 step ahead and guess around 50 ∙ p, where p is the fraction of the median that the game sets to aim. (For example, p=1/2 for the Harvard party game.) This reasoning applies recursively: if most opponents are “step κ” players, in order to outplay them, one needs to think κ + 1 steps ahead and guess around 50 . pκ+1, and so on. Given one guessed x, we can work backwards and estimate the number of steps s/he thinks ahead to be κ = logp(x/50). Thus, the winning strategy to is to estimate as accurately as possible m(κ), the median step by which the opponents are thinking ahead, and beat them by thinking precisely one step more: κ* = m(κ) + 1.
Over the years, fond memories of my serendipitous win have stimulated my curiosity. I regretted that the raw guesses were not preserved, and longed for a close look at the first-hand evidence of adaptive human thinking. Today came the perfect chance to spread the fun and recreate the data. At the Rutgers statistics department annual retreat party, held in the log cabin of Rutgers Gardens amid the beautiful fall foliage, I had the chance to administer the game to 52 new colleagues and students. The outcome was surprisingly clean: the median was 25 and its half 12.5, corresponding to m(κ)=1 and a winning strategy κ*=2. Three winners emerged from the game: two (Rong Chen and Yisha Yao) guessed 12 and one (Steven Buyske) guessed 13. Raw guesses spanned the entire allowable range, from as low as 1 to as high as 100, and are tabulated in Figure 1 in terms of individuals’ κ. It became apparent that the most fun occurs when, as in most competitive settings, one thinks just one step more than the rest—no more, no less!
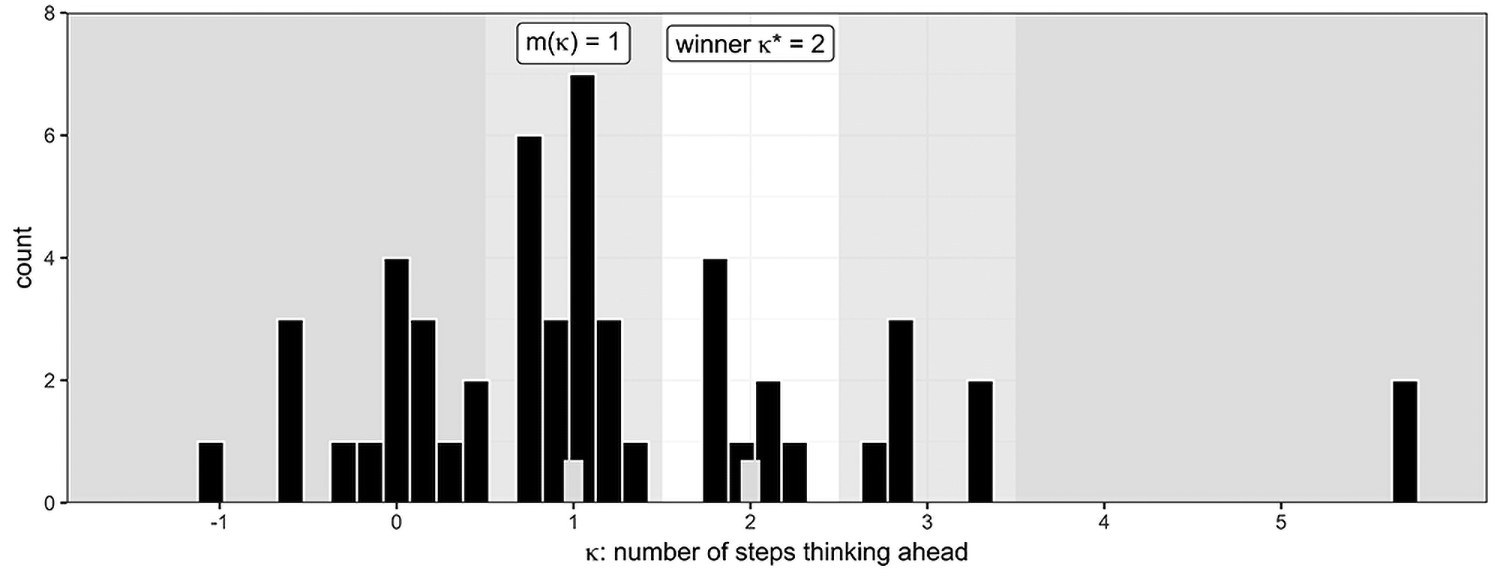
Figure 1: Guess 1/2 of the median: data from Rutgers annual retreat party (n=52). Patterns of clustering around κ values {0, 1, 2, 3}. Winning strategy is κ* = 2, corresponding to guesses 12 and 13.
Footnotes
[1] Quearly, K. ‘How readers fared in Upshot’s Number Puzzle.’ The New York Times, Aug 2015. [Online; accessed 27 October 2018].
[2] Schou, A. ‘Gœt-et-tal konkurrence afslører at vi er irrationelle.’ Politiken, Sept 2005. [Online (in Danish); accessed 27 October 2018].
[3] Wikipedia contributors. ‘Guess 2/3 of the average.’ Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Guess_2/3_of_the_average&oldid=862246390, 2018. [Online; accessed 27 October 2018].
Comments on “There’s fun in thinking just one step more”