Congratulations to Mirza Uzair Baig at the University of Hawai’i at Mānoa, who wrote an excellent solution to the problem.

Note that the statistic T_n may be represented as

$$T_n=I_{Y_{(1)}<X_{(1)},Y_{(n)}<X_{(n)}}[\sum _{i=1}^n{I}_{Y_i<X_{(1)}}+\sum _{i=1}^n{I}_{X_i>Y_{(n)}}]$$
$$+I_{X_{(1)}<Y_{(1)},X_{(n)}<Y_{(n)}}[\sum _{i=1}^n{I}_{X_i<Y_{(1)}}+\sum _{i=1}^n{I}_{Y_i>X_{(n)}}].$$

Denote the empirical CDF of $X_1,\cdots ,X_n$ by $F_n$ and that of $Y_1,\cdots ,Y_n$ by $G_n$. Then, this above representation yields

$$T_n=n{I}_{Y_{(1)}<X_{(1)},Y_{(n)}<X_{(n)}}[G_n(X_{(1)})+1-F_n(Y_{(n)})]$$ $$+n{I}_{X_{(1)}<Y_{(1)},X_{(n)}<Y_{(n)}}[F_n(Y_{(1)})+1-G_n(X_{(n)})].$$ Use the fact that for given $u,v,n{F}_n(u)$ and $n{G}_n(v)$ are binomial random variables with success probabilities $F(u)$ and $G(v)$. Now use the iterated expectation formula by conditioning on the minima and the maxima to get the mean, and similarly, but with a longer calculation, the variance. It is useful to think of $T_n$ as approximately a sum of two geometrics. Suppose $W$ is a negative binomial with parameters $r=2,p=\frac{1}{2}$. Then for $n$ not too small, $T_n$ would have a point mass at zero mixed with the negative binomial. That is, write down a Bernoulii variable $Z$ with parameter $\frac{1}{2}$; then $T_n$ (in law) is approximately $Z(W+2)$. This gives a quick explanation for why the mean and the variance under the null of $T_n$ should be about $2$ and $6$. You can see a plot below of the null distribution of $T_n$ below when $n=300$; it is distribution-free in its usual sense.

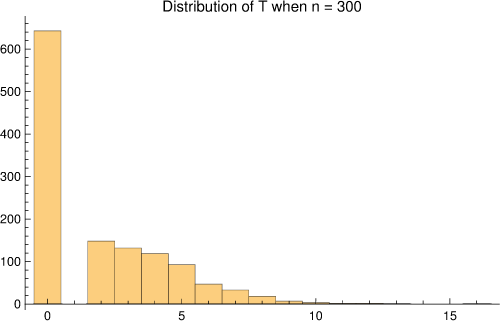
Under specified alternatives, the negative binomial would be replaced by a sum of two geometrics, approximately independent, but not i.i.d.

—

The next puzzle, number 21, is here. Can you solve it? Send us your answer by September 7.