Richard Kenyon received his PhD from Princeton University in 1990 under the direction of William Thurston. After a postdoc at IHES, he held positions at CNRS in Grenoble, Lyon, and Orsay, before becoming a professor at UBC for 3 years and then moving to Brown University where he is currently the William R. Kenan Jr. University Professor of Mathematics. He was awarded the CNRS bronze medal, the Rollo Davidson prize and the Loève prize; he is a member of the American Academy of Arts and Sciences, and is currently a Simons Investigator.

Richard Kenyon’s 2017 Schramm lecture will be given at the 39th Conference on Stochastic Processes and their Applications (SPA) in Moscow (July 24–28, 2017). See http://www.spa2017.org/

Limit shapes beyond dimers

The boxed plane partition (see Figure 1) is a tiling of a hexagon of side length $n$ by “lozenges”: tiles consisting of $60^{\circ}$ rhombi in one of the three possible orientations; one can also think of it as a projection of a stack of cubes stacked into an $n\times n\times n$ box in such a way that the surface of the stack projects monotonically to the plane $x+y+z=0$.

Fig. 1: The boxed plane partition

In the limit $n\to\infty$ under rescaling there is a well-known “limit shape phenomenon” [ref1, ref2] under which this surface in ℝ$^3$, defined by a uniform random boxed plane partition, when scaled by $n$, converges to a nonrandom surface. This surface is the unique surface spanning the boundary and minimizing a certain surface tension, which we can write as
$$\iint_{H} \sigma(\nabla h)\,dx\,dy,$$
where $H$ is the hexagon, $h:H\to$ ℝ is the function giving the height of the surface above the plane $x+y+z=0$.

There is a similar limit shape phenomenon for tilings of any other region, obtained by minimizing the surface tension with other boundary conditions [ref2, ref4].

The main tool for studying the lozenge tiling model is the determinantal formula describing the correlations between individual tiles. These are based on the formula due to Kasteleyn [ref3] which shows that the number of lozenge tilings of a simply connected polygonal region is the determinant of the adjacency matrix of an underlying graph.

In joint work with Jan de Gier and Sam Watson we consider a generalization of the lozenge tiling model, which we call the five-vertex model since it is a special case of the well-known six-vertex model in which one of the six local configurations is disallowed. This model is, concretely, a different measure on the same space of lozenge tilings: we simply give a configuration a weight probability proportional to $r$ to the power of the number of
adjacencies between two of the three types of tiles. The lozenge tiling model is the case $r=1$ of this model.

This new measure is no longer determinantal. Thus we must rely on the Bethe Ansatz method for counting the number of configurations and computing correlations. This is notoriously difficult to carry out and indeed the solution to the general six-vertex model is a well-known open problem. Somewhat remarkably, this calculation can be performed for the five-vertex model to get a complete limit shape theory: we can give an explicit PDE describing the limit shapes associated to the model.

Like the lozenge model, limit shapes are obtained by minimizing a surface tension $\sigma_r(\nabla h)$ for given boundary values. Again $\nabla h=(s,t)$ varies
over the triangle 𝒩$=cvx\{(0,0),(1,0),(0,1)\}$. The surface tension $\sigma_r:$𝒩$\to$ℝ is an explicit smooth convex function also involving the dilogarithm,
$$Li_2(z) := -\int_0^z\frac{\log(1-\zeta)}{\zeta}\,d\zeta.$$
see Figure 3. Unlike the lozenge case there is a certain curve in 𝒩
$$\gamma=\{(s,t)~:~1-s-t+(1-r^{-2})st=0\}$$
along which $\sigma$ is not analytic; for $(s,t)$ on the side of $\gamma$ near the line $s+t=1$ the underlying Gibbs measure $\mu_{s,t}$ is not extremal. Physically, we think of the paths consisting of the white and light gray lozenges as attracting each other; for typical configurations the paths clump together. On the other side of the curve these lines repel each other. The surface tension is conveniently written in terms of a pair of auxiliary complex variables $z,w$ lying on the spectral curve $0=P(z,w) = 1-z-w+(1-r^2)zw$.
The relation between $(s,t)$ and $(z,w)$ is described in Figure 2.

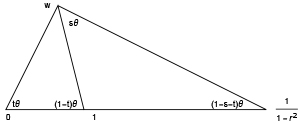
Fig. 2: Given $r$ and a point $(s,t)\in$𝒩 (on the left side of the curve $\gamma$), there is a unique $w$ in the upper half plane satisfying the property that $t = \arg(w)/\arg(\frac{w}{1-w})$ and $s=\arg(z)/\arg(\frac{z}{1-z})$. Here $\bar z$ is the reflection of $w$ in the circle of radius $r/(1-r^2)$ centered at $1/(1-r^2)$.

The Euler-Lagrange equation for the variational problem is the PDE that any minimizer will satisfy. In this case the PDE, when written in terms of the variables $z,w$ with $P(z,w)=0$, (each of which is a function of $x,y$) reduces to the wonderfully simple form
$$\frac{\partial B(w)}{\partial w} w_y – \frac{\partial B(z)}{\partial z} z_x = 0,$$
where $B(z) = \arg z\log|1-z|+ Im Li(z)$ is a nonanalytic function.

This research was supported by the NSF and the Simons foundation.

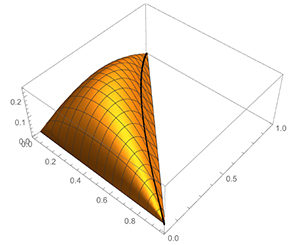
Fig. 3: Minus surface tension as a function of $(s,t)\in$𝒩 with $r=.8$. The black line is the curve $\gamma$.

References

References
[1] H. Cohn, M. Larsen, J. Propp, The shape of a typical boxed plane partition, New York J. Math. 4 (1998), 137–165.
[2] H. Cohn, R. Kenyon, J. Propp, A variational principle for domino tilings. J. Amer. Math. Soc. 14 (2001), no. 2, 297–346.
[3] P. Kasteleyn, Dimer statistics and phase transitions. J. Mathematical Phys. 4 1963 287–293.
[4] R. Kenyon, A. Okounkov, Limit shapes and the complex Burgers equation. Acta Math. 199 (2007), no. 2, 263–302.