Frank den Hollander is professor of mathematics at Leiden University in The Netherlands. His research focuses on probability theory, ergodic theory, statistical physics, population dynamics and complex networks. Frank has supervised 13 PhD students and 33 postdocs, has published 150 papers, and is the author of three monographs. He has served on strategic advisory boards across Europe, and is Fellow of the American Mathematical Society and of the Institute of Mathematical Statistics. Frank is member of the Royal Dutch Academy of Sciences. He has been awarded 25 national and international research grants, including an ERC Advanced Grant and a ten-year consortium grant by the Dutch Ministry of Education, Culture and Science called NETWORKS.
Frank’s Medallion Lecture will be delivered at the World Congress in Toronto in July 2016.
Metastability for the Widom–Rowlinson Model
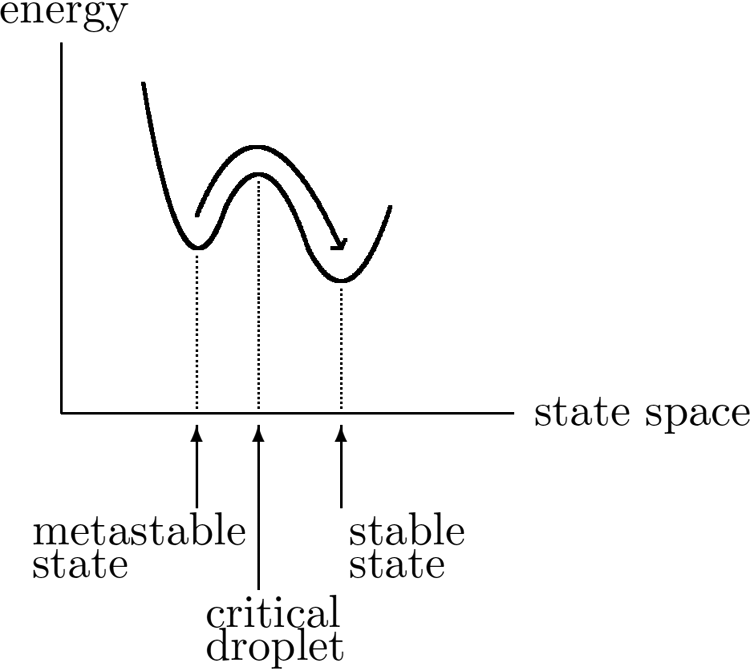
Metastability is the phenomenon where a physical system, under the influence of a stochastic dynamics, moves between different subregions of its state space on different time scales. Metastability is encountered in a wide variety of physical systems. The challenge is to devise realistic models and to explain the experimentally observed universality displayed in metastable behaviour, both qualitatively and quantitatively. For an overview, see the monograph by Bovier and den Hollander1.
In statistical physics, metastability is the dynamical manifestation of a first-order phase transition. An example is condensation. When water vapour is cooled down slightly below 100 degrees Celsius, it persists for a very long time in a metastable vapour state before transiting to a stable liquid state under the influence of random fluctuations. The crossover occurs after the system manages to create a critical droplet of liquid inside the vapour, which once present grows and invades the system. While in the metastable vapour state, the system makes many unsuccessful attempts to form a critical droplet, because this requires the system to climb an ‘energetic hill’.
In the static Widom–Rowlinson model5, particles are viewed as points carrying disks, and the energy of a particle configuration equals minus the total overlap of the disks (consequently, the interaction between the particles is attractive). It was shown by Ruelle4 and by Chayes, Chayes and Kotecky2 that, on the infinite Euclidean space, this model has a first-order phase transition between a vapour state and a liquid state. The phase transition occurs as the chemical potential, controlling the density of the particles, changes from a subcritical value to a supercritical value. The model is therefore a natural candidate to display metastable behaviour.

Above: Particles interacting via overlap of their disks
The dynamic Widom–Rowlinson model on a two-dimensional torus is considered in den Hollander, Jansen, Kotecky and Pulvirenti3. Particles are randomly created and annihilated as if the outside of the torus were an infinite reservoir with a given chemical potential. The system evolves according to a Metropolis dynamics associated with the Hamiltonian H of the model, i.e., a move from an old to a new conguration is accepted at rate $\exp[-\beta (\Delta H)_+],$
with $\beta \in (0,\infty)$ the inverse temperature and $(\Delta H)_+$ the positive part of the change in the Hamiltonian caused by the move ($H$ depends both on the energy and on the chemical potential).
We are interested in the metastable behaviour at low temperature when the chemical potential is supercritical. In particular, we start with the empty torus (which represents the vapour state) and are interested in the first time when we reach the full torus, i.e., the torus is fully covered by disks (which represents the liquid state). In order to achieve the transition from empty to full, the system needs to create a sufficiently large droplet of overlapping disks, which plays the role of the critical droplet that triggers the crossover. In the limit as $\beta\to\infty$ (low-temperature limit), we compute the asymptotic scaling of the average crossover time, show that the crossover time divided by its average is exponentially distributed, and identify the size and the shape of the critical droplet.
The critical droplet turns out to be close to a disk of radius
$R_c(\kappa) = \frac{2\kappa}{\kappa-1},$
where κ ∈ (1,∞) is a parameter controlling the degree of supercriticality of the chemical potential. The average crossover time scales like
exp[βU(Rc(κ))−β1/3S(Rc(κ))+o(β1/3)], β→∞.
The leading term corresponds to the classical Arrhenius law, with U(Rc(κ)) the energy of the critical droplet. The correction term, which is large, represents a substantial deviation from this law, with S(Rc(κ)) the entropy of the critical droplet. This correction term comes from the fact that the boundary of the critical droplet is ‘bumpy’, with many particles sticking out just a little. It turns out that there are ≍β particles inside the critical droplet, ≍β1/3 particles touching the boundary, while the boundary itself fluctuates on scale β−1/2.
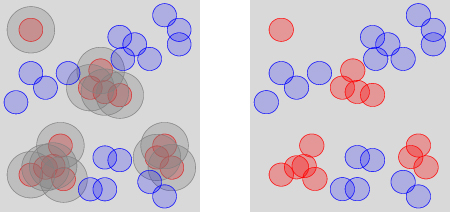
Above: The one-species model as the projection of the two-species model.
The Widom–Rowlinson model can be viewed as the projection of a two-species model with hard-core repulsion in which one of the species is not observed. It therefore also serves as a model for phase separation.
References:
1 A. Bovier, and F. den Hollander, Metastability—A Potential–Theoretic Approach, Grundlehren der mathematischen Wissenschaften, Volume 351, Springer, 2015.
2 J.T. Chayes, L. Chayes, and R. Koteck´y, The analysis of the Widom–Rowlinson model by stochastic geometric methods, Commun. Math. Phys. 172, 551–569 (1995).
3 F. den Hollander, S. Jansen, R. Kotecky, and E. Pulvirenti, Metastability for the Widom–Rowlinson model, work in progress. [supported by ERC Advanced Grant 267356-VARIS]
4 D. Ruelle, Existence of a phase transition in a continuous classical system, Phys. Rev. Lett. 27, 1040–1041 (1971).
5 B. Widom and J.S. Rowlinson, New model for the study of liquid–vapor phase transitions, J. Chem. Phys. 52, 1670–1684 (1970).

1 comment on “Medallion lecture preview: Frank den Hollander”