Jeffrey S. Rosenthal, Professor of Statistics, University of Toronto, writes:

It happens to the instructor of every university-level introductory statistics class. You define the mean m, and the variance v. You explain how to estimate the mean from an i.i.d. sample, via $\overline{x}=\frac{1}{n}\sum x_i$. Then you have to explain how to estimate the variance. Nervously you write down the usual estimate, $s^2=\frac{1}{n-1}\sum (x_i-\overline{x}{)}^2$. At which point, every student in the class raises their hand, and asks, “Why do you divide by n−1, instead of by n?”

You then have a choice. You can awkwardly explain that this division “will be explained later”. Or you can protest that if n is large then “it doesn’t really matter”. Or you can mystically muse that “if n=1 then the answer should be undefined, not zero”. Or you can launch into a confusing and premature explanation of unbiased estimators, which at that stage will enlighten almost no one. (The situation is so dire that some instructors refuse to teach s² at all, cf. [1].) Meanwhile, the students would prefer to simply divide by n, corresponding to taking an average value, which everyone understands. So why can’t they?

The usual answer, of course, is that s² is an unbiased estimator of v, i.e. E(s²)= v. And everyone knows that unbiased estimators are so important that they trump any concerns about simplicity or comprehensibility.

Or do they? In preparing my teaching this year, I started to question this assumption. After all, the true value of an estimator is how accurately it estimates. And the best way to measure the accuracy of an estimate is through the mean squared error (MSE). Now, the MSE is the sum of the bias squared plus the estimator’s variance. If the estimator is unbiased, then the bias term is zero, which is good. But could this come at the expense of increasing the estimator’s variance, and hence increasing its MSE? Perhaps yes!

For a simple example, suppose a true parameter is 8, and our estimator equals either 6 or 10 with probability $\frac{1}{2}$ each. Then the estimator is unbiased, with MSE = $2^2$ = 4. Now, suppose we instead “shrink” our estimator by some factor r (slightly less than 1), so it equals either 6r or 10r with probability $\frac{1}{2}$ each. Then the MSE = $\frac{(10r-8{)}^2+(8-6r{)}^2}{2}$

If $r$=0.95, then MSE=3.77, significantly less than 4. That is, a smaller, shrunken, biased estimator actually reduces the MSE here.

This example suggests the possibility, at least, that $\frac{1}{n-1}\sum (x_i-\overline{x}{)}^2$ might not have the smallest possible MSE after all—and perhaps the more natural estimator $\frac{1}{n}\sum (x_i-\overline{x}{)}^2$ has a smaller MSE!

Fortunately, such calculations have already been done (see e.g. [2]). Indeed, if $v$ is estimated by $\frac{1}{a}\sum (x_i-\overline{x}{)}^2$ for any $a>0$, then the MSE is known to be

$\frac{n-1}{n{a}^2}[(n-1)\gamma +n^2+n]v^2-(\frac{2(n-1}{a}-1)v^2$

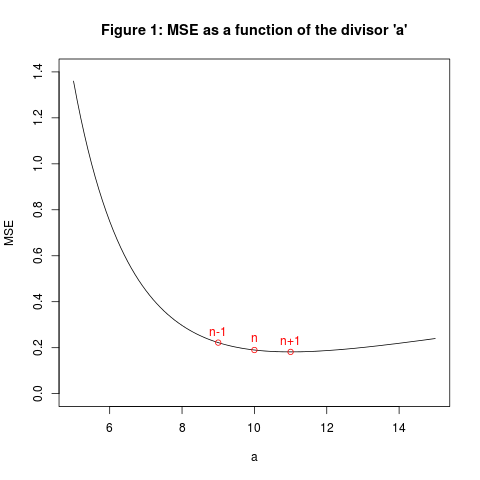
where $\gamma =E[(X_1-m{)}^4]/v^2-3$ is the excess kurtosis. If the $X_i$ are Gaussian, then $\gamma =0$, and the MSE is smaller when $a=n$ than when $a=n-1$; in fact the MSE is minimised when $a=n+1$ (not when $a=n-1$). See Figure 1 below for the case $v=1$ and $\gamma =0$ and $n=10$.

So, the next time I explain estimating the variance, I am going to divide by $n$, not by $n-1$. This will save a lot of confusion, and make much more sense to the students. It’s true that my estimator will be biased, but it will still have a smaller MSE than yours. Besides, there will be plenty of time to discuss unbiased estimators later on. And the next time your students want to divide by $n$ rather than $n-1$, well, the kids are alright.

References
[1] D.J. Rumsey (2009), Let’s just eliminate the variance. Journal of Statistics Education 17(3). Available at: www.amstat.org/publications/jse/v17n3/rumsey.html
[2] Wikipedia, Mean squared error: Variance. Retrieved August 26, 2015. Available at: en.wikipedia.org/wiki/Mean_squared_error#Variance. (See also www.probability.ca/varmsecalc).