The Student Puzzle Corner contains one or two problems in statistics or probability. Sometimes, solving the problems may require a literature search. Current student members of the IMS are invited to submit solutions electronically (to bulletin@imstat.org with subject “Student Puzzle Corner”). Deadline EXTENDED to November 1, 2014. The names and affiliations of (up to) the first 10 student members to submit correct solutions, and the answer(s) to the problem(s), will be published in the next issue of the Bulletin. The Editor’s decision is final.
Student Puzzle Corner 6
We will try to approach a difficult statistics problem in this issue. It does not necessarily involve any difficult mathematics; but the problem is inherently unstable.
It has been surmised, and even seriously investigated, whether neolithic man was in possession of a so-called quantum. A quantum is simply a positive number $q$ such that a certain set of similar measurements follow the mathematical formula $x = qn$ for some positive integer $n$. In words, all your measurements are multiples of a fixed basic unit, called the quantum. Alexander Thom and David Kendall have done profound and highly original studies of whether the diameters of neolithic monuments in Scotland, Wales, and England follow a quantum pattern. The evidence is seductive and interesting, but it is difficult to formulate the problem and draw conclusions— particularly because 4,000 years have passed since the stones were originally put there. If indeed neolithic man had a quantum, it may be reasonable to ask whether the quantum had a significance, and how it was passed from generation to generation and from one area to another… but these questions are outside the domain of mathematics.
So, in this issue’s problem, we have taken a subset of a famous science dataset and converted the original numbers ni, all positive integers, by following the formula
$x_i = qn_i + є_i , i = 1, 2, …, n = 50$.
The є_i are random errors with zero mean. We do not tell you what quantum $q$ we used, and we do not tell you what is the exact distribution of the random errors. The question asked is: can you estimate the quantum $q$? The answer must describe a rational attack and method of solution, not merely a one-sentence numerical guess. As we said, it is not going to be easy to come within a close shot of the true quantum!
The dataset is:
1.00, 7.21, 13.92, 17.81, 22.00, 24.88, 27.08, 32.74, 37.36, 39.36, 45.66, 47.32, 53.6, 55.02, 61.46, 63.05, 69.3, 77.24, 80.5, 79.68, 89.83, 96.48, 101.99, 103.81, 110.34, 111.61, 117.16, 118.99, 127.25, 130.34, 140.05, 145.19, 150.36, 158.03, 160.25, 168.21, 170.07, 176.59, 178.87, 181.74, 186.49, 192.79, 195.08, 202.4, 205.06, 212.46, 215.95, 224.28, 229.9, 238.9.
A word of caution: note that the data values have been reported to two digits after the decimal. So you can get a spurious perfect fit by using a small quantum, e.g., q = .01!
Solution to Student Puzzle 5
Anirban DasGupta, IMS Bulletin Editor, explains:
Colman Humphrey (pictured below) of the Wharton School at the University of Pennsylvania gave a sensible formulation of the last issue’s problem and sent a rigorous and correct solution for his formulation. We encourage more of our student members to send solutions!

Here is a slightly different formulation. Let $N$ denote the number of children a random couple in this country has, and let $B, G$ denote their number of boy and girl children; thus, $B+G = N \sim \mathcal{P}(\lambda ), \lambda > 0$. Suppose that each conception results in one boy with probability $p$ or one girl with probability $q, p+q = 1, 0 < p < 1$.
Under the usual assumptions, one has $B \sim \mathcal{P}(\lambda p), G \sim \mathcal{P}(\lambda q)$, and $B, G$ are independent Poissons. Basically, if events are arriving according to a Poisson process and then falling into one of $k$ mutually exclusive counters, then the counts of each counter are also Poisson processes with the obvious rates, and these $k$ Poisson processes are independent.
In our problem, the Mitchells do have at least one boy, namely Dennis; we know that $B \geq 1$. Dennis has $B-1$ other brothers and $G$ sisters. We want to know when is $P(B-1 = G|B \geq 1) \geq \frac{1}{2}$?
Now, after a few lines of algebra,
\[ P(B-1 = G|B \geq 1) \]
\[ = \frac{\sum_{j = 1}^\infty P(B = j, G = j-1)}{P(B \geq 1)} \]
\[ = \frac{\frac{e^{-\lambda }}{\lambda q}\,\sum_{j = 1}^\infty
\frac{(\lambda ^2pq)^j}{j!(j-1)!}}{1-e^{-\lambda p}} \]
\[ = \frac{\lambda p\,e^{-\lambda }\,\sum_{j = 0}^\infty
\frac{(\lambda \sqrt{pq})^{2j}}{j!(j+1)!}}
{1-e^{-\lambda p}} \]
\[ = \sqrt{\frac{p}{q}}\,\frac{e^{-\lambda }I_1(\lambda \,
\sqrt{4pq})}{1-e^{-\lambda p}}, \]
where $I_1(z)$ is the modified Bessel function of the first kind of index one. For the general index $\nu, -\infty < \nu < \infty $, the modified Bessel function $I_{\nu }(z)$ may be defined by the infinite series
\[ I_{\nu }(z) = (\frac{z}{2})^{\nu }\, \sum_{j = 0}^\infty
\frac{(\frac{z^2}{4})^{j}}{j!\,\Gamma (j+\nu + 1)}. \]
For the special case $p = \frac{1}{2}$, we have the reduction
\[ P(B-1 = G|B \geq 1) = \frac{e^{-\lambda }\,I_1(\lambda )}{1-e^{-\lambda /2}}. \]
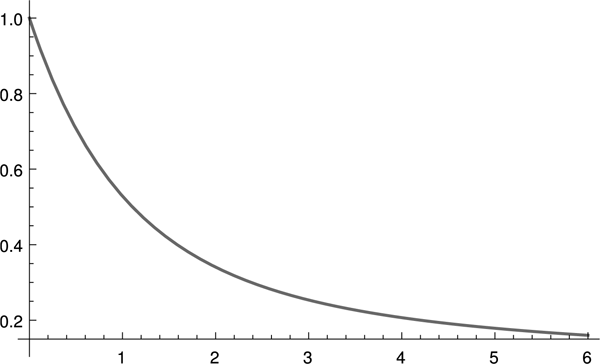
This is $.5$ or more for $\lambda \leq 1.10626 \approx 1.11$.
So, the answer to the narrow question of the problem of the previous issue is that we should bet that Dennis has an equal number of brothers and sisters if we know that $\lambda $ is smaller than about $1.11$.
\[ P(B-1 = G|B \geq 1)\]
Comments on “Student Puzzle Corner 6 (deadline now November 1)”