Contributing Editor Anirban DasGupta writes:
Lazily leafing through the pages of the 2012 World Almanac, I noticed a curiously common phenomenon. Be it the deserts, lakes, mountain peaks, rivers, or waterfalls in the world, or buildings, bridges, tunnels, books, operas, space expeditions—the most spectacular ones are visibly more impressive than the rest. Act of nature or act of man, there is a hidden non-Gaussian who appears to like a second mode at the far right tail.

These provide interesting and challenging problems statistically. First, we cannot possibly have a complete dataset for any of these constructs; so, one has an unknown number of missing values, and at best, one can study distributions that are left truncated (Woodroofe, 1985, AOS; Gross and Lai, 1996, JASA). Second, these measurements are often not universally agreed on, or even almost impossible to make very accurately. And, third, to explain bi-modality or heavy tails, one really must look into the science of the variable; for example, if the most awesome mountain peaks are strikingly more regal in their heights, what underlying geology is driving the upper tail?

Today, in this one-page column, let me first state a few little tidbits. For example, I noticed that even leaving aside the Caspian sea, the four biggest continental lakes are on average twice as big as the next biggest one, Lake Tanganyika. Not counting the polar deserts, the biggest desert—the Sahara—is about four times as large as the very next one. The Khone waterfall, the widest on our planet, flowing off the Mekong river, is twice as wide as the very next one, the Pará in Venezuela. The Gamma ray burst with the largest energy, recorded on April 27, has about 3 times more energy than the next record. Coming to human achievements, the three largest buildings in the world are on an average 7 million sq. ft. larger than the very next one; the three longest bridges in the world are on an average 40 miles longer than the fourth-longest bridge. Based on bone fragment estimates, the tallest man ever alive, excavated at a Neolithic French cemetery, was at least 2 feet taller than anyone who ever lived (La Nature, v. 18, 1890). And, one can go on.

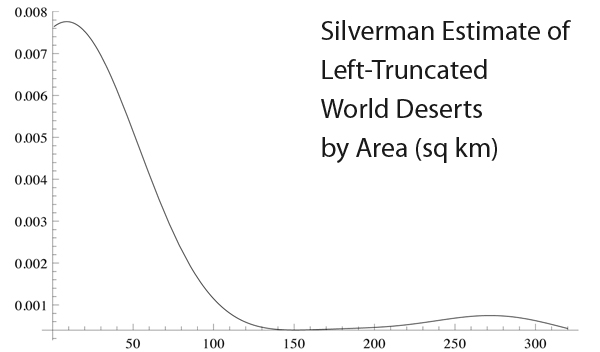
To the naked eye, these were clusters of outliers, indicative of heavy tails, mixture, or bimodality. Just to feed my curiosity, I tried my hand at a little classic kernel density estimation à la Rosenblatt (1956, AMS) and Parzen (1962, AMS). I obtained carefully defined left-truncated data on three constructs of nature (height of mountain peaks, areas of deserts, widths of waterfalls), and three constructs of Man (floor space of buildings, total length of bridges, and duration of human expeditions to the International Space Station). I took all the data from Wikipedia. Left truncation is a constraint of the form X ≥ a; the Wikipedia articles clearly define the cutoff a. For example, when it comes to nonpolar deserts, the cutoff was 50,000 sq. kms.

Density estimation is mired in complexities to do with bandwidth choice and other details (e.g., Scott, 1992, Wiley; Hall et al., 1991, Biometrika). Not to be too finicky, I decided to use a Gaussian kernel and the Silverman reference bandwidth $h$ = 1.06 $s$ $n^{−1/5}$ (1986, C&H). Sensitivity analysis would be interesting, but I have no room for it here. When I obtained the kernel density plots, I did notice a clear second mode at the very extreme tail. Sometimes it was a loud second mode, and sometimes an audible whisper. But it was always there. Was this a spurious bump? I couldn’t tell for sure. But I did generate a truly Gaussian sample of comparable n to my cases here, and then applied Silverman’s rule on the truncated Gaussian data. The second mode did not show up. One of the densities is produced here:

If a second mode at the extreme upper tail is not a phantom mode, one would crave an explanation. A broad brush explanation might be that achievement scores would always tend to produce a small proportion of dazzling outliers; no surprises there. This might be true, but it isn’t an intellectually satisfying explanation. We must ask, why? For instance, the tallest mountain peaks are all located in the Himalayan range, with a few in the Karakoram. Is it the case that the geologic process giving rise to the Himalayas 250 million years ago contributed to the extraordinarily high and majestic peaks? Do global economy and political choices have something to do with a bundle of astonishingly large structures and buildings confined to a few middle eastern countries and China?

Only when I understand the cause of that second mode can I be happy that I have really understood an applied statistics question I looked at nonchalantly so far.